概述
伸展树是一种能够自我平衡的二叉查找树,它能在均摊O(log n)的时间内完成基于伸展操作的插入、查找、修改和删除操作。它是由丹尼尔·斯立特(Daniel Sleator)和罗伯特·塔扬在1985年发明的。 ——— 维基百科
伸展树是基于这样的事实,当一个节点被访问时,它就很可能不久再被访问到。
伸展树的基本想法是,当一个节点被访问后,它就要经过一系列AVL树的旋转被放到根上。注意,如果一个节点很深,那么在其路径上就存在许多的节点也相对较深,通过重新构造可以使对所有这些节点的进一步访问所花费的时间变少。因此,如果节点过深,那么我们还要求重新构造应具有平衡这棵树(到某种程度)的作用。 ———— 《数据结构与算法分析 ——c语言描述》
缺点
伸展树在经过一系列伸展操作后,有可能会变成一条链。
操作
伸展
当一个节点x被访问后,伸展操作会将x移动到根节点。为了进行伸展操作,我们会进行一系列的旋转,每次旋转,会使x离根更近。
每次旋转由三个因素决定:
- x是其父节点p的左儿子还是右儿子
- p是否为根
- p是其父节点g(x的祖父节点)的左儿子还是右儿子
Zig标记为元素是父节点的左儿子,Zag标记为元素是父节点的右儿子。
共有四种情况
x没有父节点和祖父节点,x为根
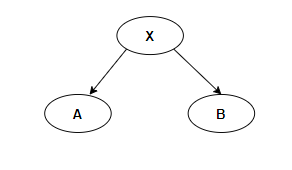
如图所示,不需要旋转
Zig或Zag
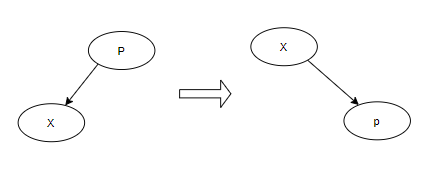
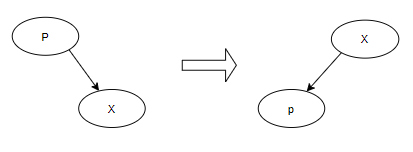
如图所示,P为根,X为P的左子树或者右子树,则只需要进行对应方向的单旋转即可
Zig-Zig 或 Zag-Zag
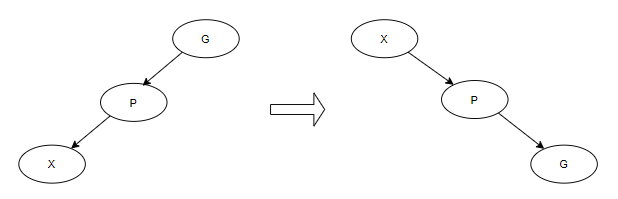
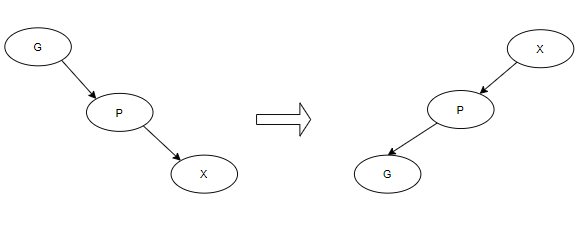
当p为G的左节点且x为p的左节点,或反之。如图所示进行旋转。
Zig-Zag 或 Zag-Zig
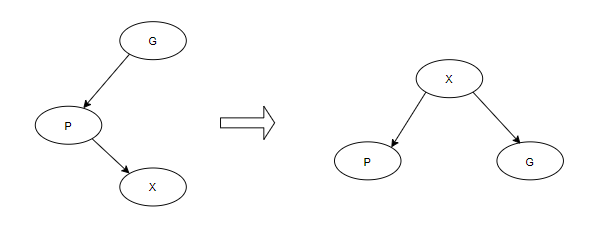
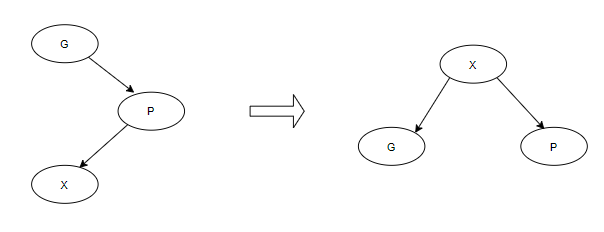
当p为G的左节点且x为p的右节点,或反之。如图所示进行变换。
连接
给出两棵树S和T,且S的所有元素都比T的元素要小。下面的步骤可以把它们连接成一棵树:
- 伸展S中最大的节点。现在这个节点变为S的根结点,且没有右儿子。
- 令T的根结点变为其右儿子。
分割
给出一棵树和一个元素X,返回两棵树:一棵中所有的元素均小于等于X,另一棵中所有的元素大于X。下面的步骤可以完成这个操作:
- 伸展X。这样的话X成为了这棵树的根所以它的左子树包含了所有比X小的元素,右子树包含了所有比X大的元素。
- 把X的右子树从树中分割出来。
实现
伸展
伸展操作有两种实现方式:top-down和down-top,即自上而下和自下而上。我们可以把伸展的所有情况都拆分成左单旋和右单旋的基本操作。
自上而下(top-dpwm)
自上而下是一种相对容易的实现方式,并不需要记录查找路径中所有节点的信息,查找的同时进行旋转操作。
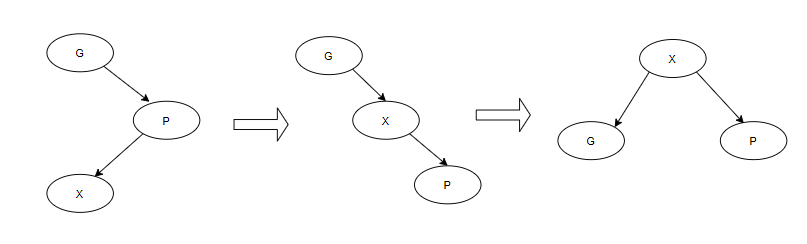
如图所示,在Zag-Zig情况中,我们可以对旋转步骤进行分解,先对X进行右旋操作,再对X进行左旋操作
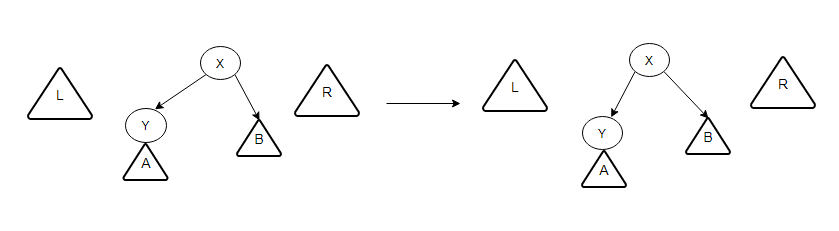
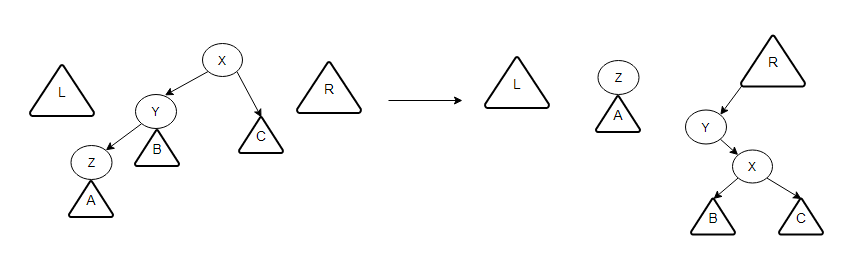
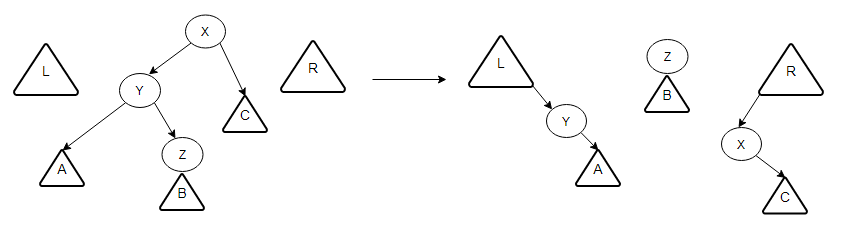
如上图所示,分别表示了在自上而下的实现方式中,单旋转、一字型旋转及之字形旋转的变换过程。
伸展方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| SplayTree Splay(Position x, TElemType e)
{
SplayNode Header;
Position LeftTreeMax, RightTreeMin;
Header.left = Header.right = NULL;
LeftTreeMax = RightTreeMin = &Header;
while (e != x->data) {
if (e < x->data) {
if (x->left == NULL) break;
if (e < x->left->data)
x = SingleRotateWithLeft(x);
if (x->left == NULL) break;
/* 链接右树 */
RightTreeMin->left = x;
RightTreeMin = x;
x = x->left;
}
else {
if (x->right == NULL) break;
if (e > x->right->data)
x = SingleRotateWithRight(x);
if (x->right == NULL) break;
LeftTreeMax->right = x;
LeftTreeMax = x;
x = x->right;
}
}
LeftTreeMax->right = x->left;
RightTreeMin->left = x->right;
x->left = Header.right;
x->right = Header.left;
return x;
}
|
代码中Header存放伸展后左子树和右子树的基址。
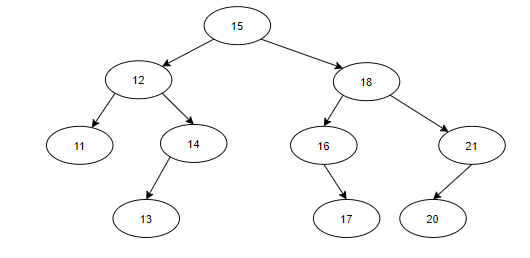
如图所示,如果要伸展的值为13,则需要进行如下判断。首先,x<15,则将节点15放入RightTreeMin中,RightTreeMin为节点12。然后x>12,则将节点12放入LeftTreeMax中,依次类推。
即表示,只要x大于当前元素的值,就放入LeftTreeMax中。只要x小于当前元素的值,就放入RightTreeMin中。伸展操作最后,进行连接操作,将LeftTreeMax置为x的左孩子,RightTreeMin置为x的右孩子。
单旋操作
见Zig或Zag图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| Position SingleRotateWithLeft(Position K2)
{
Position K1;
K1 = K2->left;
K2->left = K1->right;
K1->right = K2;
return K1;
}
Position SingleRotateWithRight(Position K1)
{
Position K2;
K2 = K1->right;
K1->right = K2->left;
K2->left = K1;
return K2;
}
|
自下而上(down-top)
在自下而上的操作过程中,我们需要先找到x,然后再递归向上伸展,需要记录查找路径中节点的信息。
伸展操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| void Splay(Position x)
{
Position p;
Position g;
while (x->parent) {
if (!x->parent->parent) {
if (x == x->parent->left) {
SingleRotateWithLeft(x->parent);
}
else {
SingleRotateWithRight(x->parent);
}
}
else {
p = x->parent;
g = p->parent;
// zig-zig
if (x == p->left && p == g->left) {
SingleRotateWithLeft(g);
SingleRotateWithLeft(p);
}
// zig-zag
if (x == p->left && p == g->right) {
SingleRotateWithLeft(p);
SingleRotateWithRight(g);
}
// zag-zig
if (x == p->right && p == g->left) {
SingleRotateWithRight(p);
SingleRotateWithLeft(g);
}
// zag-zag
if (x == p->right && p == g->right) {
SingleRotateWithRight(g);
SingleRotateWithRight(p);
}
}
}
}
|
旋转操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
void SingleRotateWithLeft(Position x)
{
Position y;
y = x->left;
x->left = y->right;
if (y->right != NULL) {
y->right->parent = x;
}
y->parent = x->parent;
// x is root of the tree
if (x->parent == NULL) {
T = y;
} else if (x == x->parent->left) {
x->parent->left = y;
}
else {
x->parent->right = y;
}
y->right = x;
x->parent = y;
}
void SingleRotateWithRight(Position x)
{
Position y;
y = x->right;
x->right = y->left;
if (y->left != NULL) {
y->left->parent = x;
}
y->parent = x->parent;
// x is root of the tree
if (x->parent == NULL) {
T = y;
}
else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
|
参考链接











